本博客前面文章已对图有过简单的介绍，本文主要是重点介绍有关图的一些具体操作与应用

阅读本文前，可以先参考本博客

各种基本算法实现小结（四）—— 图及其遍历

一、无向图

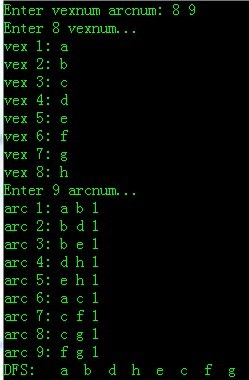
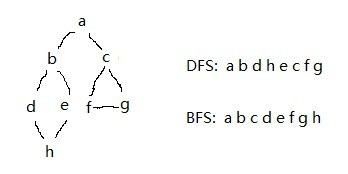
1 无向图——邻接矩阵

测试环境：VS2008

<br /> #include "stdafx.h"<br /> #include <stdlib.h><br /> #include <malloc.h><br /> #define MAX_VEX 20<br /> #define INFINITY 65535<br /> int *visited;<br /> struct _node<br /> {<br /> int vex_num;<br /> struct _node *next;<br /> };<br /> typedef struct _node node, *pnode;<br /> struct _graph<br /> {<br /> char *vexs;<br /> int arcs[MAX_VEX][MAX_VEX];<br /> int vexnum, arcnum;<br /> };<br /> typedef struct _graph graph, *pgraph;<br /> int locate(graph g, char ch)<br /> {<br /> int i;<br /> for(i=1; i<=g.vexnum; i++)<br /> if(g.vexs[i]==ch)<br /> return i;<br /> return -1;<br /> }<br /> graph create_graph()<br /> {<br /> int i, j, w, p1, p2;<br /> char ch1, ch2;<br /> graph g;<br /> printf("Enter vexnum arcnum: ");<br /> scanf("%d %d", &g.vexnum, &g.arcnum);<br /> getchar();<br /> for(i=1; i<=g.vexnum; i++)<br /> for(j=1; j<g.vexnum; j++)<br /> g.arcs[i][j]=INFINITY;<br /> g.vexs=(char *)malloc(sizeof(char));<br /> printf("Enter %d vexnum.../n", g.vexnum);<br /> for(i=1; i<=g.vexnum; i++)<br /> {<br /> printf("vex %d: ", i);<br /> scanf("%c", &g.vexs[i]);<br /> getchar();<br /> }<br /> printf("Enter %d arcnum.../n", g.arcnum);<br /> for(i=1; i<=g.arcnum; i++)<br /> {<br /> printf("arc %d: ", i);<br /> scanf("%c %c %d", &ch1, &ch2, &w);<br /> getchar();<br /> p1=locate(g, ch1);<br /> p2=locate(g, ch2);<br /> g.arcs[p1][p2]=g.arcs[p2][p1]=w;<br /> }<br /> return g;<br /> }<br /> int firstvex_graph(graph g, int i)<br /> {<br /> int k;<br /> if(i>=1 && i<=g.vexnum)<br /> for(k=1; k<=g.vexnum; k++)<br /> if(g.arcs[i][k]!=INFINITY)<br /> return k;<br /> return -1;<br /> }<br /> int nextvex_graph(graph g, int i, int j)<br /> {<br /> int k;<br /> if(i>=1 && i<=g.vexnum && j>=1 && j<=g.vexnum)<br /> for(k=j+1; k<=g.vexnum; k++)<br /> if(g.arcs[i][k]!=INFINITY)<br /> return k;<br /> return -1;<br /> }<br /> void dfs(graph g, int i)<br /> {<br /> int k, j;<br /> if(!visited[i])<br /> {<br /> visited[i]=1;<br /> printf("%3c", g.vexs[i]);<br /> for(j=firstvex_graph(g, i); j>=1; j=nextvex_graph(g, i, j))<br /> if(!visited[j])<br /> dfs(g, j);<br /> }<br /> }<br /> void dfs_graph(graph g)<br /> {<br /> int i;<br /> visited=(int *)malloc((g.vexnum+1)*sizeof(int));<br /> for(i=1; i<=g.vexnum; i++)<br /> visited[i]=0;<br /> for(i=1; i<g.vexnum; i++)<br /> if(!visited[i])<br /> dfs(g, i);<br /> }<br /> int _tmain(int argc, _TCHAR* argv[])<br /> {<br /> graph g;<br /> g=create_graph();<br /> printf("DFS: ");<br /> dfs_graph(g);<br /> printf("/n");<br /> return 0;<br /> }<br />

运行结果：

==========================================================

2




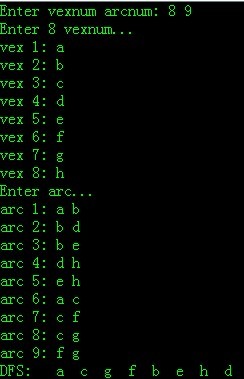
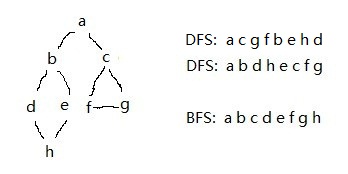
无向图——




邻接表

测试环境：VS2008

<br /> #include "stdafx.h"<br /> #include <stdlib.h><br /> #include <malloc.h><br /> #define MAX_VEX 20<br /> int *visited;<br /> typedef struct _ArcNode<br /> {<br /> int ivex; /* next ivex */<br /> struct _ArcNode *nextarc; /* next node */<br /> int *info; /* arc weight */<br /> };<br /> typedef struct _ArcNode ArcNode, *pArcNode;<br /> struct _VNode<br /> {<br /> char adjvex; /* note vex */<br /> ArcNode *firstarc;<br /> };<br /> typedef struct _VNode VNode;<br /> struct _ALGraph<br /> {<br /> VNode AdjList[MAX_VEX];<br /> int vexnum, arcnum;<br /> int kink;<br /> };<br /> typedef struct _ALGraph ALGraph;<br /> int locate(ALGraph g, char ch)<br /> {<br /> int i;<br /> for(i=1; i<=g.vexnum; i++)<br /> if(g.AdjList[i].adjvex==ch)<br /> return i;<br /> return -1;<br /> }<br /> ALGraph create_graph()<br /> {<br /> int i, j, w, p1, p2;<br /> char ch1, ch2;<br /> pArcNode pnode, pnode1, pnode2;<br /> ALGraph g;<br /> printf("Enter vexnum arcnum: ");<br /> scanf("%d %d", &g.vexnum, &g.arcnum);<br /> getchar();</p> <p> printf("Enter %d vexnum.../n", g.vexnum);<br /> for(i=1; i<=g.vexnum; i++)<br /> {<br /> printf("vex %d: ", i);<br /> scanf("%c", &g.AdjList[i].adjvex);<br /> getchar();<br /> g.AdjList[i].firstarc=NULL;<br /> }<br /> printf("Enter arc.../n");<br /> for(i=1; i<=g.arcnum; i++)<br /> {<br /> printf("arc %d: ", i);<br /> scanf("%c %c", &ch1, &ch2);<br /> getchar();<br /> p1=locate(g, ch1);<br /> p2=locate(g, ch2);<br /> pnode1=(pArcNode)malloc(sizeof(ArcNode));<br /> pnode2=(pArcNode)malloc(sizeof(ArcNode));<br /> pnode1->ivex=p2; /* next ivex */<br /> pnode1->nextarc=g.AdjList[p1].firstarc;<br /> g.AdjList[p1].firstarc=pnode1;<br /> pnode2->ivex=p1; /* next ivex */<br /> pnode2->nextarc=g.AdjList[p2].firstarc;<br /> g.AdjList[p2].firstarc=pnode2;<br /> }<br /> return g;<br /> }<br /> int firstvex_graph(ALGraph g, int i)<br /> {<br /> int k;<br /> if(i>=1 && i<=g.vexnum)<br /> if(g.AdjList[i].firstarc)<br /> return g.AdjList[i].firstarc->ivex;<br /> return -1;<br /> }<br /> int nextvex_graph(ALGraph g, int i, int k)<br /> {<br /> pArcNode pnode;<br /> if(i>=1 && i<=g.vexnum && k>=1 && k<=g.vexnum)<br /> {<br /> pnode=g.AdjList[i].firstarc;<br /> while(pnode->nextarc)<br /> {<br /> k=pnode->nextarc->ivex;<br /> if(!visited[k])<br /> return k;<br /> else<br /> pnode=pnode->nextarc;<br /> }<br /> }<br /> return -1;<br /> }<br /> void dfs(ALGraph g, int i)<br /> {<br /> int k;<br /> if(!visited[i])<br /> {<br /> visited[i]=1;<br /> printf("%c", g.AdjList[i].adjvex);<br /> for(k=firstvex_graph(g, i); k>=1; k=nextvex_graph(g, i, k))<br /> if(!visited[k])<br /> dfs(g, k);<br /> }<br /> }<br /> void dfs_graph(ALGraph g)<br /> {<br /> int i;<br /> visited=(int *)malloc((g.vexnum+1)*sizeof(int));<br /> for(i=1; i<=g.vexnum; i++)<br /> visited[i]=0;<br /> for(i=1; i<=g.vexnum; i++)<br /> if(!visited[i])<br /> dfs(g, i);<br /> }<br /> int _tmain(int argc, _TCHAR* argv[])<br /> {<br /> ALGraph g;<br /> g=create_graph();<br /> dfs_graph(g);<br /> printf("/n");<br /> return 0;<br /> }<br />

运行结果：

==========================================================