KMP算法，Knuth-Morris-Pratt Algorithm，一种由Knuth(D.E.Knuth)、Morris(J.H.Morris)和Pratt(V.R.Pratt)三人提出的一种快速模式匹配算法。

KMP 朴素算法

原理：

子串pattern依次与目标串target中的字符比较，如果相等，继续比较下一个字符；如果不等，pattern右移一位，重新开始比较，直至匹配正确或超出target。

示例：

子串 pattern={aabaa}，目标串target={aababaacaabaa}，比较过程如下图：

特点：

思路简单、代码直观；但效率低、有回溯、不够简洁、时间复杂度高

// 在target中查找子串pattern的起始位置，pos初始为0
int index(char *target, char *pattern, int pos)
{
	if(NULL == target || NULL == pattern){
		return -1;
	}

	int k = pos, j = 0;
	while(k<strlen(target) && j<strlen(pattern)){		// 未超出字符串长度
		if(target[k] == pattern[j]){					// 字符相同，则继续向后比较
			k++;		
			j++;
		}else{											// 如果不同，则回溯重新查找	
			k = k - j + 1;
			j = 0;
		}
	}

	if(j == strlen(pattern)){						// 如果找到，则返回字串起始位置(首次匹配)
		return k - strlen(pattern);
	}else{											// 如果没找到，则返回-1
		return -1;
	}
}

小结：

在最坏的情况下，每次比较都在最后一个字符出现不等（如aaaaaaaaaaaaab和ab）

假设pattern长度为m，target长度为n，则每趟最多比较m次，最多循环比较（n-m）趟，总比较次数为m*(n-m)，即时间复杂度为O（m*n）

KMP 算法的演变

我们由上面KMP朴素算法的例子来引出一个问题。

为了便于问题分析，令P（pattern），T（target），字符数组下标从0开始。通过仔细分析，发现P（Pattern）前4个字符是匹配的，只有最后一个字符P[4]不匹配！

如果P右移1位，P前两字符

aa

又将与T（target）的

ab

不匹配

如果P右移2位，P第一个字符

a

就与T的

b

不匹配

如果P右移3位，P前两字符

aa

又将于T的

ab

不匹配（同右移1位的情况）

如果P右移4位，P第一个字符

a

就与T的

b

不匹配（同右移2位的情况）

如果P右移5位，即P跨过已经与T比较过的五位了，省去了右移1、2、3、4位的步骤

为什么是5位呢？我们再深入分析，转换思考问题的侧重点，发现5位字符正好是P（Pattern）子串的长度，是不是P子串本身就蕴含了模式匹配的奥秘？

答案是肯定的！

P： aaba

a(X)

注意：最后一个字符不匹配，即a(X)

上图直观给出，P要么右移3位，要么右移5位，才有可能与T（target）出现匹配。

我们探索P本身的规律，发现P（aabaa）移位的大小，与其自身的首尾覆盖特性有关，即aa—b—aa（移3位跳过b字符，移5位跳过自身，从头开始比较）

于是我们引出了另外一个问题——覆盖函数

什么是覆盖函数呢？

我们直接给出定义：

对于序列

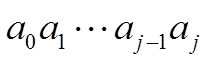
找出这样一个k，使其满足

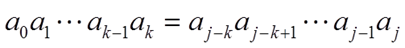
并且要求k尽可能的大！（原因后面再讲）

求P自身最大的k值，对于P（pattern）的前j序列字符(从下标0计起)，有两种可能：

1、 pattern[j] == pattern[preOverlay+1] 时，overlay(j) = preOverlay + 1 = overlay(j-1) + 1

2、 pattern[j] !=  pattern[preOverlay+1] 时，overlay(j)需要在前preOverlay中找；使preOverlay = overlay[preOverlay]，重复2过程

// 求pattern覆盖
void overlay_Pattern(const char *pattern)
{
	const int len = strlen(pattern);
	int *overlay = new int[len];
	int i, preOverlay;

	overlay[0] = -1;
	for(i=1; i<len; i++){
		preOverlay = overlay[i-1];

		while (preOverlay >= 0 && pattern[i] != pattern[preOverlay+1]){
			preOverlay = overlay[preOverlay];
		}

		if (pattern[i] == pattern[preOverlay+1]){
			overlay[i] = preOverlay + 1;
		}else{
			overlay[i] = -1;
		}
	}

	for(i=0; i<len; i++){
		printf("%d\n", overlay[i]);
	}

	delete []overlay;
}

示例：

例如P： aabaa  其overlay依次为：-1、0、-1、0、1

-1表示没有覆盖，0表示有一个覆盖，1表示有两个覆盖，从-1开始计起

再如P：

abaabcabab  其overlay依次为：-1、-1、0、0、1、-1、0、1、2、1

KMP算法

KMP算法，是由KMP朴素算法演变而来的，主要分为两步：

第一步，当字符串比较出现不等时，确定下一趟比较前，应该将子串pattern右移多少个字符（预处理）

第二步，子串pattern右移后，应该从哪个字符开始和目标串target中刚才比较时不等的那个字符继续开始比较（查找）
 

下面给出完整的KMP算法：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>


// 预处理子串
void kmp_Prepare(char *target, char *pattern, int *overlay)
{
	memset(overlay, 0, sizeof(overlay));

	int i = -1, j = 0, preOverlay;
	overlay[0] = -1;

	for(i=1; i<strlen(pattern); i++){
		preOverlay = overlay[i-1];
		
		while(preOverlay >= 0 && pattern[i] != pattern[preOverlay+1]){
			preOverlay = overlay[preOverlay];
		}

		if(pattern[i] == pattern[preOverlay+1]){
			overlay[i] = preOverlay + 1;
		}else{
			overlay[i] = -1;
		}
	}

	for(i=0; i<strlen(pattern); i++){
		printf("overlay[%d]: %d\n", i, overlay[i]);
	}
}

// 查询子串
int kmp_Find(char *target, char *pattern, int *overlay)
{
	int index_pattern = 0;
	int index_target = 0;

	while(index_pattern < strlen(pattern) && index_target < strlen(target)){
		if(target[index_target] == pattern[index_pattern]){
			index_target++;
			index_pattern++;
		}else if(index_pattern == 0){
			index_target++;
		}else{
			index_pattern = overlay[index_pattern - 1] + 1;
		}
	}

	if(index_pattern == strlen(pattern)){
		return index_target - index_pattern;
	}else{
		return -1;
	}
}



int main(int argc, char **argv)
{
	char *target = "aababaacaabaa";
	char *pattern = "aabaa";
	int *overlay = new int[strlen(pattern)];

	int index_s = -1;

	printf("target: %s, len: %d\n", target, strlen(target));
	printf("pattern: %s, len: %d\n", pattern, strlen(pattern));

	kmp_Prepare(target, pattern, overlay);
	index_s = kmp_Find(target, pattern, overlay);

	printf("index_s: %d\n", index_s);

	getchar();
	return 0;
}

测试示例：

pattern： aabaa

target：  aababaacaabaa

运行结果：

总结：

第一步，其实就是KMP朴素算法对模式匹配子串pattern的预处理过程，上面已经给出了算法公式和代码示例

第二步，本质上就是KMP朴素算法，不同的仅仅是pattern右移的位数大小由其预处理过程决定
 

KMP算法不太容易理解，但其简洁、高效，时间复杂度为O(m+n)

其中，O(m)是pattern子串预处理的时间复杂度，

O(n)是target目标串查找的时间复杂度，总时间复杂度为O(m+n)

KMP代码下载

参考推荐：

KMP（百度百科）

Knuth-Morris-Pratt algorithm（Wikipedia）

Knuth-Morris-Pratt algorithm（String Matching）

Knuth-Morris-Pratt string matching

原文： KMP字符串匹配算法