各种基本算法实现小结(四)——图及其遍历
各种基本算法实现小结(四)—— 图及其遍历
(均已测试通过)
====================================================================
图——深度优先和广度优先算法
无向图用二维邻接矩阵表示
测试环境:VC 6.0 (C)
运行结果:
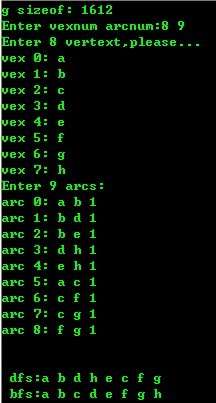
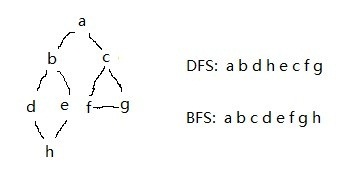
======================================================
图——深度优先
测试环境:VS2008 (C)
======================================================
图——广度优先
测试环境:VS2008 (C)
======================================================
图——深度优先和广度优先算法2(网摘)
本文引用网址:http://bbs.bccn.net/thread-155311-1-1.html(编程论坛)
看到本算法在网上转载较多,比较流行,且能直接运行
但发现大多转载中,也把DFS与BFS正好写反了,对此本文已修正
此外,本算法混用了C与C++,不够单纯,申请的指针空间也未及时释放
测试环境:VC 6.0 (C)
运行结果:
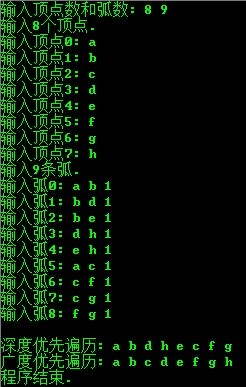
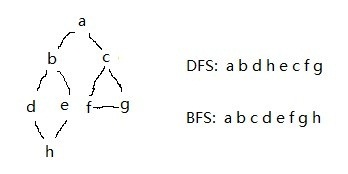
======================================================
参考推荐:
版权所有: 本文系米扑博客原创、转载、摘录,或修订后发表,最后更新于 2010-06-03 21:53:55
侵权处理: 本个人博客,不盈利,若侵犯了您的作品权,请联系博主删除,莫恶意,索钱财,感谢!