各种基本算法实现小结(七)——常用算法
各种基本算法实现小结(七)—— 常用算法
(均已测试通过)
======================================================================
1、判断素数
测试环境:VC 6.0 (C)
运行结果:
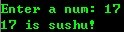

==========================================================
2、 求2-1000之间的所有素数
测试环境:VC 6.0 (C)
运行结果:
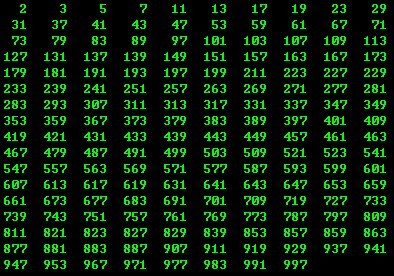
==========================================================
3、 验证哥德巴赫猜想
哥德巴赫猜想:
任意一个大于等于6的偶数都可以分解为两个素数之和
如: 6 = 3+3;100 = 3+97=11+89; 1000 = 3+997=59+941=。。。
测试环境:VC 6.0 (C)
运行结果:


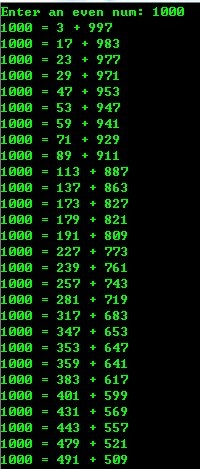
==========================================================
4、 求最大公约数(GCD)和最小公倍数(LCM)
测试环境:VC 6.0 (C)
运行结果:

==========================================================
5、统计个数(数字)
用随机函数产生100个[0,99]范围内的随机整数,
统计个位上的数字分别为0,1,2,3,4,5,6,7,8,9的数的个数并打印出来
测试环境:VC 6.0 (C)
运行结果:
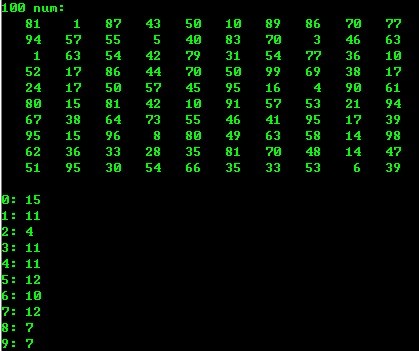
==========================================================
6、统计个数(数字、字符、其它字符)
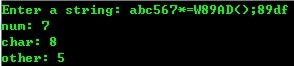
输入一行字符,统计其中有多少个数字、字符和其它字符
测试环境:VC 6.0 (C)
运行结果:
==========================================================
7、 数制转换(递归实现)
本算法仅实现了基数为2-16的数制转换
如果大家希望扩展范围,仅需要对基数表示字符case 进行扩展即可,如G、H、I ...
测试环境:VC 6.0 (C)
运行结果:
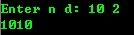
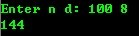
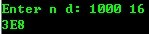
算法改进
数制直接转为字符输出,扩展支持16进制以上的数制转换
运行结果
(扩展进制):
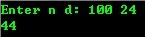
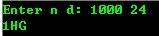
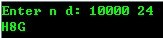
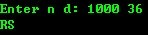
100 = 4*24+4 1000=1*24*24+17*24+16 10000=17*24*24+8*24+16 1000=27*36+28
==========================================================
8、 数制转换(栈实现)
核心思想和递归实现类似,都是压栈的原理,实现较简单,请自己尝试实现
==========================================================
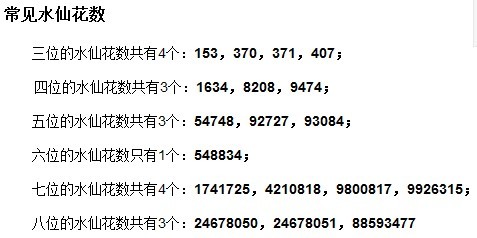
9、 水仙花数
水仙花数简述:
水仙花数是指一个 n 位数 ( n≥3 ),它的每个位上的数字的 n 次幂之和等于它本身。
如:153=
1
^3+
5
^3+
3
^3(3位数);1634=
1
^4+
6
^4+
3
^4+
4
^4(4位数);54748=
5
^5+
4
^5+
7
^5+
4
^5+
8
^5(5位数)
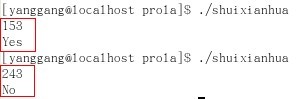
判断任一3位数,是否为水仙花数
测试环境:GCC
运行结果
(Redhat Linux):
================================================
求4位数的水仙花数(1000<=X<=9999)
测试环境:VC 6.0 (C)
运行结果:

================================================
思考:
如果求得高精度大数的水仙花数,如8位、18位、28位的水仙花数(需考虑计算机精度,可采用数组或指针实现,大数计算)
==========================================================
10、 大数计算
大数运算
:参加的值和计算结果通常是以上百位数,上千位数以及更大长度之间的整数运算,早已超出了计算机能够表示数值的精度范围(2^32=4294967296或2^64=18446744073709551616)即64位机最大也才20位,因此需要想出其它的办法计算大数。
求任意两整数之和(1000位以内)
测试环境:VC 6.0 (C)
运行结果:

思考:
请大家自己设计实现更复杂的大数减法、乘法、除法,求余、求幂、求最小公倍数等大数运算(提示:可用数组或链表)
==========================================================
参考推荐:
版权所有: 本文系米扑博客原创、转载、摘录,或修订后发表,最后更新于 2010-06-03 21:56:10
侵权处理: 本个人博客,不盈利,若侵犯了您的作品权,请联系博主删除,莫恶意,索钱财,感谢!